La Esbeltez en Columnas y el Estudio del Equilibrio
Se describirá el estudio del equilibrio para una columna de material elástico, lineal y homogéneo, idealmente rectilínea y con carga perfectamente centrada.
Se coloca una perturbación “f” y se supone una deformación sinusoidal entre los puntos de inflexión de la deformada elástica. Para analizar el equilibrio de la misma se representa gráficamente el momento flector externo e interno para distintos estados de deformación de la pieza.
Aplicamos la carga P1, y obligamos a la pieza a salir de la posición idealmente rectilínea, se produce un momento externo: Me = P1xf que varía linealmente con f para una carga P1 constante. En la figura (a) P1 resulta igual a la pendiente de la recta de momento externo Me.
Por otro parte para cada estado de deformación, se puede definir una curvatura χ, asociada a un momento flector interno.
(Sólo para f pequeño)
Como se supone que la deformación es sinusoidal entre los puntos de inflexión de la elástica:
Perturbación lateral sinusoidal
Curvatura de la columna
Momento interno resistente
Que resulta también proporcional a “f”.
Se denomina carga crítica de pandeo o de Euler al valor:
Con lo cual no queda
Momento externo solicitante
Ecuación de equilibrio: Mi=Me (momento interno = momento externo)
Esta condición nos lleva a tres situaciones:
1) Para una carga P1 < Pc; Mi > Me siempre, por lo que al quitar la perturbación, la columna vuelve a la posición original rectilínea, por lo tanto existe equilibrio estable.
2) Para una carga P1=Pc; Mi=Me el equilibrio se vuelve equilibrio indiferente y podemos aumentar f hasta la rotura seccional de la pieza Mu.
3) Para P1 > Pc; será equilibrio inestable, ya que para cualquier perturbación Mi < Me.
La figura (b) resume gráficamente las posiciones de equilibrio posibles para una carga P dada.
 | |||||||||||
| Esbletes en Columnas - Figura: la derecha es (a) y la izquierda es (b). |
En la figura siguiente se presenta el comportamiento de una columna con una carga aplicada con una excentricidad inicial “e”. La columna en este caso deforma por si sola hasta que f = f1 para una carga P1 pues Mi < Me1, hasta su deformación. Si se saca a la columna de esa posición, y luego se hace cesar la perturbación de la columna vuelve a ella pues Mi < Me, el equilibrio es estable.
La figura (b) destaca que para una carga P = Pc no es posible alcanzar el equilibrio ya que la flecha f tiende a infinito y se alcanza la rotura o falla del material para cierto valor de f.
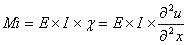


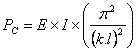



No hay comentarios:
Publicar un comentario